Chapitre
II- Quelques expériences déterminantes de
la physique ____________________________________________________
"Mieux vaut lutter pour
accéder à une compréhension complète de l’Univers que désespérer de l’esprit
humain"
Stephen
HAWKING,
31 mars
1993
table des matières de la page :
1. Le phénomène de diffraction
avec Grimaldi (1665)
2. Le phénomène des
interférences avec des fentes d’YOUNG (1803)
5. L’expérience de FRANK &
HERTZ (1914)
7. L’expérience de GERMER
& DAVISSON (1927)
9. L’expérience de STERN &
GERLACH
____________________________________________________
1. Le phénomène de diffraction avec Grimaldi (1665)

Figure 1 : Schéma de l'expérience de diffraction par une fente
La distance L, séparant la fente de l’écran, est très
grande.
On réserve en général le terme de diffraction au phénomène dans lequel
une onde rencontre un obstacle de dimensions comparables à sa longueur d’onde.
Dans l’expérience schématisée ci-dessus, un faisceau
parallèle de lumière monochromatique de longueur d’onde l arrive de la gauche sur une plaque dans laquelle on a pratiqué une fente,
perpendiculaire au plan de figure, de largeur d. La lumière passant pas cette
fente, est détectée sur un écran placé à une distance L très grande de la
fente. Le détecteur utilisé, une plaque
photographique par exemple, est sensible à l’intensité reçue en chaque oint du
plan.
1.
Si d>>l, on observe sur l’écran
une tache lumineuse conforme au
principe de la propagation rectiligne de la lumière.
2.
Si d @ ou plus petit que l, il se produit de manière
notable, le phénomène de diffraction. Pour donner une application numérique,
les ondes dans le visible ont un l de l’ordre de 0,4-0,8 mm ;le phénomène de
diffraction devient visible dès que la largeur de la fente devient inférieure à
10-15 mm.
On observe un maximum très intense pour q=0, qui contient environ 90% de
l’intensité totale, et des maxima secondaires, beaucoup moins intenses et
disposés symétriquement autour du maximum principal. On peut calculer le champ
électrique en chaque point de l’écran. L’intensité mesurée est proportionnelle
à la valeur moyenne dans le temps (prise sur une période par exemple) du carré
du module du champ électrique. Le résultat est le suivant :
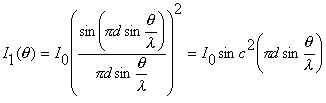
où I0 est
la valeur de l’intensité maaximum en x=0=q. On observe des minima
pour dsinq=±nl avec n=1, 2, 3, …
et des maxima moins intenses pour :
![]()
NB : lorsque d<l, on ne peut observer qu’une
partie de la tache centrale de diffraction, les valeurs de sinq devant toujours être =< 1.
De façon générale, le figure de diffraction obtenue après
un obstacle de dimension d a une dimension angulaire de l’ordre de l/d. Pour un trou circulaire de
diamètre d, la figure de diffraction est circulaire et l’angle qm, entre la position centrale et
le premier minimum, est donné par![]() .
.
Si d=10mm et l=0,6mm (radiation jaune), on a qm@0, 072 rad @ 4,2°. A 1 m du trou, le
rayon de la tache est de l’ordre de 7,3 cm.
2. Le phénomène des interférences avec des fentes d’YOUNG (1803)

Figure 2 : Expérience des fentes de Young
Si D est plus grand que d, alors nous pouvons observer le
phénomène d’interférences que nous allons décrire et qui est illustré sur la figure ci-dessus. Comme dans
le cas d’un phénomène de diffraction, nous avons des maxima et des minima
d’intensité lumineuse, mais cette fois les zones lumineuses et les zones
obscures, appelées franges d’interférence, sont très fines, serrées et équidistante les unes des
autres. Les bandes lumineuses sont aussi plus intenses que dans le phénomène de
diffraction. Les interférences résultent de la superposition des ondes
lumineuses émises par les deux sources cohérentes que constituent les deux
fentes percées dans la plaque On observe des interférences constructives
lorsque les deux ondes sont en phase en
un point de la plaque ; et elles sont destructives dans le cas contraire.
La séparation angulaire entre les maxima d’intensité lumineuse est de l’ordre
de![]() , où D est la distance séparent les deux fentes et l la longueur d’onde de la
radiation. On trouve le résultat suivant :
, où D est la distance séparent les deux fentes et l la longueur d’onde de la
radiation. On trouve le résultat suivant :

où I0 est toujours l’intensité maximale
correspondant à la diffraction par une seule fente : ![]() .
.
On observe :
1.
Des oscillations rapides dues au terme cos²![]() qui ne dépendent que de la distance D entre les deux
fentes : ce sont les franges d’interférence dont nous avons parlé plus
haut. La séparation angulaire entre les maxima ou les minima est de l’ordre de
qui ne dépendent que de la distance D entre les deux
fentes : ce sont les franges d’interférence dont nous avons parlé plus
haut. La séparation angulaire entre les maxima ou les minima est de l’ordre de ![]() .
.
2.
Enveloppant les oscillations précédentes, la courbe enveloppe comme on
l’appelle en mathématiques oscille plus lentement. Sa largeur ne dépend que de
la longueur d de chaque fente. La séparation angulaire entre les maxima ou les
minima est de l’ordre de ![]() .
.
Pour que les oscillations soient observables dans la
pratique, il faut que l soit un peu plus petit
que D. Ainsi pour observer des interférences avec des rayons X dont la longueur
d’onde est de l’ordre de 100 pm, il faut pouvoir disposer de sources cohérentes
séparées d’une distance de d l’ordre de quelques centaines de pm.
Un cristal, qui est un assemblage régulier d’atomes,,
convient parfaitement pour ce travail. Chacun de ses atomes diffuse les ondes
qu’il reçoit et se comporte comme une source cohérente de lumière. Si l’on se
place loin du cristal, on observe des interférences entre les ondes provenant
de plans réticulaires différents : c’est ce que l’on appelle la diffraction de Bragg. Cette méthode est utilisée en cristallographie pour
étudier la structure des cristaux. La figure de diffraction, appelée diagramme de LAUE (1942), permet de
déduire la structure du cristal et de mesurer la distance séparant les atomes.
La diffraction des rayons X est également utilisée en biologie moléculaire, et
elle a permis en particulier d’établir la structure en hélice de l’ADN.
3. L’effet ZEEMAN (1896)
L’observation du dédoublement des raies spectrales en
trois composantes par un champ magnétique (une raie à plus haute fréquence, une
à plus basse fréquence et une à fréquence inchangée) a fourni une des premières
estimations du rapport charge/masse de l’électron (une autre estimation ayant été
faite par Thomson et Kelvin)
En 1896, ZEEMAN découvre que lorsqu’un spectre
atomique est émis par une lampe soumise à un champ magnétique suffisamment
élevé, chaque raie spectrale se divise en plusieurs composantes polarisées linéairement
ou circulairement, avec des décalages en fréquence qui ne correspondent pas au
calcul classique. Ce dédoublement est très général et peut être résumé comme
l’action d’un champ électromagnétique sur les niveaux quantiques d’un système
subatomique S (ion, atome, métal, défaut de Frenkel, …) et pas voie de conséquence, sur les radiations
électromagnétiques en interaction avec S. Le cas où le dédoublement se fait en
trois raies est appelé effet de Zeeman normal, tandis que si le dédoublement se fait en plus de trois
composantes, l’effet sera appelé effet de Zeeman anormal.

Figure 3 : dédoublement des raies par effet ZEEMAN normal et anormal
On va supposer que les transitions entre les niveaux a et b et entre b et g respectivement sont permises, mais que la transition "directe"
entre a et g est interdite par une règle de sélection. Comme les niveaux d’énergie sont
fonction de B, la fréquence de raies spectrales correspondantes dépend
aussi de B (déplacement ZEEMAN). Dans l’exemple de la figure 8, certains niveaux comme g restent simples en présence
d’augmentation de B et on dira alors qu’ils sont non dégénérés. D’autres comme a et b vont se dédoubler quand B va augmenter, et on dira alors qu’ils
sont respectivement quadruplement et triplement dégénérés en l’absence de
champ, et que l’application de B lève leur dégénérescence. De la même
manière que les transitions entre niveaux successifs est permise, les
transitions entre sous niveaux successifs sont permises, du moment qu’elles
sont en accord avec les règles de transition.
a) En champ faible (normal)
b) En champ fort (anormal)
(A suivre)
4. L’effet PASCHEN-BACK
(à suivre !)
5. L’expérience de FRANK & HERTZ (1914)
Expérience décisive d’absorption d’énergie des électrons
par des atomes de mercure, dont les résultats furent présentés en 1914 pour
montrer la quantification des niveaux d’énergie prédite par Bohr. Elle consiste
à bombarder de la vapeur de Hg par des électrons accélérés sous une différence
de potentiel de l’ordre de quelques dizaines de volts.

Figure 4 : Expérience de Frank et Hertz
La figure 8 représente le diagramme schématique de
l’expérience : une triode est remplie de vapeur de Hg sous faibles
pression (1 mm), et un filament à la cathode émet des électrons. Un électron va
arriver à la grille G avec l’énergie maximum EM=eV0 s’il n’a pas fait de
collisions sur le parcours filament-grille. S’il fait une ou plusieurs collisions, alors deux cas
apparaissent :
1.
collision élastique : les électrons passent la grille G et sont collectés sur
la plaque P et l’on détecte une augmentation du courant i dans l’ampèremètre I.
2.
collision inélastique : si V0 dépasse un certain seuil VR,
les électrons vont céder eVR dans une collisions au détriment de leur
énergie cinétique et en conséquence ils ne pourront plus atteindre la plaque P,
d’où une diminution du courant ;on observe ensuite des effets provenant de
feux collisions successives, etc.
6. L’effet COMPTON (1923)
1904. Lors d’expériences de diffusion
de rayons X par la matière, on a commencé à constater que ceux-ci étaient émis
dans toute les directions. Il faut comprendre que bien que de nos jours cette
diffraction peut sembler évidente (un rayon X n’est autre qu’une onde
électromagnétique comme la lumière, à seule différence de sa longueur d’onde et
fréquence, par conséquent, il semble naturel que les rayons X se difractent, de
la même manière que la lumière) ; de ce temps la, on classait les
différents types d’ondes électromagnétiques suivant leur pouvoir e pénétration
dans la matière : plus le rayons pouvaient traverser de matière, plus ils
étaient dits "durs" et réciproquement "mous") . On avait
remarqué lors de ces expériences de diffusion que les rayons diffusés
contiennent des composantes molles et que celles-ci se divisaient en deux
catégories :
- une partie dépend de a lumière
diffusante (phénomène de fluorescence).
- l’autre parte…bah, on ne sait
pas alors expliquer son origine ne fait !
1909. BARKLA reprend ces
expériences et constate les deux choses suivantes :
- la diffusion est plus
importante en avant que en arrière.
- plus les radiations sont
orientées vers l’arrière, plus elles sont molles.
g2
1912. LAUE prouve en étudiant
cette diffusion à travers un cristal que ces radiations sont des ondes électromagnétiques
de longueur d’onde comprise entre quelques angströms et quelques dizaines
d’angströms.
1914. BRAGG apporte un support plus théorique en démontrant ce
qui deviendra la fameuse formule de BRAGG : nl = 2asina qui permet de déterminer la distance
a entre les plans réticulaires d’un cristal lorsque l’on connaît la longueur
d’onde des rayons X incidents.
1923. Cette dernière expérience va
permettre à COMPTON de reprendre les expériences de BARKLA en mesurant la
longueur d’onde des rayons X diffusés. Le dispositif expérimental est présenté
à la figure suivante. q est un angle quelconque
suivant lequel on fait l’observation

Figure 5 : Dispositif du l'expérience de Compton
7. L’expérience de GERMER & DAVISSON (1927)
Cette expérience va permettre de confirmer l’hypothèse de
DE BROGLIE suivant laquelle toute particule a un comportement
ondulatoire, et par conséquent il serait donc possible d’observer des
phénomènes de diffraction en partant d’un faisceau de corpuscules. C’est bien ce que DAVISSON et GERMER ont
constaté lorsqu’ils réalisèrent la première expérience de diffraction d’un
faisceau d’électrons monocinétiques par un monocristal de nickel.

Figure 6 : Expérience de DAVISSON ET GERMER
Envoyons un
faisceau de rayons X sur une poudre cristalline . On remarque alors, après
développement de la plaque photographique faisant écran des anneaux de
diffraction appelés anneaux de DEBYE-SCHERRER qui sont
parfaitement décrits par la formule de BRAGG citée plus haut : nl=2asin(b/2) où a est
la distance entre les plans
réticulaires du cristal et n est l’odre des anneaux.
Recommençons
maintenant l’expérience en envoyant sur la poudre cristalline un faisceau monocinétique d’électrons :
on constate alors que l’on observe une figure de diffraction semblable à celle
observée avec les rayons X. Cette expérience est la confirmation de l’existence
d’une onde associée aux électrons. De surcroit, si on mesure la quantité de
mouvement p des électrons et leur longueur d’onde l à partir des anneaux de diffraction, on trouve : l=h/p.
Cette
remarque expérience permet de se faire une idée concrète des hypothèses
fructueuses de Louis DE BROGLIE.
8. L’effet TCHERENKOV (1934)
Introduction. Cet effet apparaît lorsque des
particules voyagent plus vite que la lumière dans un milieu réfringent et transparent,
en provoquant une sorte de bang super sonique dans le champ électromagnétique :

Figure 7 : l'effet TCHERENKOV
Le
passage de particules chargées à travers la matière donne lieu à des
interactions de natures diverses, l'une d'elles étant l'émission de radiation
électromagnétique appelée effet Tcherenkov.
Dans les milieux transparents, cet effet apparaît sous la forme d'un éclair de
lumière dont les rayons sont émis dans des directions liées à la trajectoire et
à la vitesse de la particule. Cette émission très particulière revêt certaines
caractéristiques des ondes de choc qui ne se produisent que lorsque la vitesse
de la particule dépasse la vitesse de la lumière dans ce milieu.
Les
particules fournies par les accélérateurs des centres de recherche ou provenant
du rayonnement cosmique ne sont observables que par leurs interactions. L'effet
Tcherenkov en est une et sert de base à des méthodes aussi précises que variées
de mesure des propriétés de ces particules. Il est à l'origine de nombreuses
découvertes (dont celle de l'antiproton), et la plupart des expériences de
physique des particules fondamentales font appel à des détecteurs Tcherenkov
dont nous parlerons brièvement ci-dessous.
Dès
les débuts de la radioactivité, on avait observé que les solutions de sels de
radium émettent une faible lueur bleutée. Le rayonnement nucléaire d'une
préparation de radium au voisinage de liquides ou de solides transparents
suffit à provoquer cette émission de lumière. MALLET L. avait déjà montré vers 1929 que cet
effet n'était pas une luminescence, mais c’est aux physiciens TCHERENKOV
Pavel Alexeïevitch et VAVILOV
Sergey Ivanovich que revient l'honneur d'avoir
établi à partir de 1934 les propriétés fondamentales de ce phénomène qui ont
mené à son interprétation:
§
l'émission de lumière se produit dans
tous les liquides ou solides transparents sous la forme d'un spectre continu,
contrairement aux phénomènes de phosphorescence;
§
la lumière, fortement polarisée, est
émise dans la direction du rayonnement en provenance de la préparation
radioactive.
Guidés
par ces données expérimentales, les théoriciens russes FRANK Ilya M. et TAMM Igor Ievghenievitch proposèrent une théorie qui, s'appuyant sur
l'électrodynamique classique, expliquait toutes les propriétés observées de
cette radiation et en prédisait même de nouvelles.
Description. Lorsqu'une particule
chargée se déplace dans un milieu transparent (verre, liquide, gaz), ce
déplacement agit sur les champs électrique et magnétique comme une série
d'éclairs successifs; un peu comme les lampes d'une guirlande qui s'allument à
tour de rôle, donnant l'impression qu'elles se déplacent le long du fil de
support. Dans tout phénomène vibratoire, et la lumière en est un, une série de
tops ou d'éclairs est équivalente à une série de sources émettant également sur
toutes les fréquences, chacune étant décalée différemment dans le temps. Ce
décalage Dt introduit pour chaque
fréquence n et pour chaque source un
décalage de phase Dj = 2.p. n.Dt. Dans notre cas, le décalage en temps
est le temps que met la particule pour aller d'un point à un autre de sa
trajectoire, c'est-à-dire le temps L/v, L étant la longueur parcourue
dans le milieu transparent et v la vitesse de la particule. Si un
observateur regarde la particule venant vers lui avec un angle q, il verra ces sources fictives
avec un retard supplémentaire dû au temps que met la lumière pour venir jusqu'à
lui. Ce retard diminue quand la particule se rapproche. Ainsi, cet observateur
verra une série de sources ou d'éclairs émettant successivement et se décalant
comme ![]() , où c est la vitesse de la lumière dans le vide et
, où c est la vitesse de la lumière dans le vide et ![]() la vitesse de la
lumière dans notre milieu transparent, n étant l'indice de réfraction du
milieu. Lorsque la particule a une vitesse supérieure à la vitesse de la
lumière dans le milieu transparent, on peut trouver un angle d'observation pour
lequel ces deux effets se compensent exactement:
la vitesse de la
lumière dans notre milieu transparent, n étant l'indice de réfraction du
milieu. Lorsque la particule a une vitesse supérieure à la vitesse de la
lumière dans le milieu transparent, on peut trouver un angle d'observation pour
lequel ces deux effets se compensent exactement:![]() . Alors, toutes les sources fictives sont synchronisées, il
peut y avoir détection de lumière et il y a émission de lumière Tcherenkov.
Dans tous les autres cas, les variations des champs électrique et magnétique en
provenance des sources agissent en désordre et s'annulent globalement par
interférence, et rien n'est visible. La condition d'émission Tcherenkov s'écrit
habituellement:
. Alors, toutes les sources fictives sont synchronisées, il
peut y avoir détection de lumière et il y a émission de lumière Tcherenkov.
Dans tous les autres cas, les variations des champs électrique et magnétique en
provenance des sources agissent en désordre et s'annulent globalement par
interférence, et rien n'est visible. La condition d'émission Tcherenkov s'écrit
habituellement:![]() , où
, où ![]() . Cet angle q pour lequel la condition
est réalisée s'appelle l'angle Tcherenkov. Une telle condition ne peut exister
que si v > c/n, autrement dit si la vitesse de la particule
est plus grande que la vitesse de la lumière dans le milieu. Cette condition
est impossible à réaliser dans le vide où n = 1.
. Cet angle q pour lequel la condition
est réalisée s'appelle l'angle Tcherenkov. Une telle condition ne peut exister
que si v > c/n, autrement dit si la vitesse de la particule
est plus grande que la vitesse de la lumière dans le milieu. Cette condition
est impossible à réaliser dans le vide où n = 1.
La
lumière Tcherenkov est directement liée aux constantes fondamentales de la physique.
Toutes ces caractéristiques sont connues. Comme l'indice de réfraction est
facile à mesurer par des méthodes classiques, la lumière Tcherenkov permet une
mesure directe de la vitesse des particules. Les équations de Maxwell, qui
lient les charges électriques en mouvement au champ électrique et magnétique,
sont les seules nécessaires pour décrire complètement le phénomène.
Le phénomène est dû à la brusque apparition d'un courant
ou d'une charge en mouvement en un point de l'espace. Le champ électrique est
donc dans le plan contenant la trajectoire et l'observateur, le champ
magnétique est perpendiculaire à ce plan. La lumière est totalement polarisée.
L'intensité lumineuse est donnée par le produit des projections des champs
électrique et magnétique sur le plan perpendiculaire à la ligne de propagation
de la lumière. Cela donne immédiatement une dépendance en sin2q du nombre de photons émis. Les
équations de Maxwell sont simples lorsqu'on considère des fréquences fixes. Elles donnent la valeur exacte du flux
d'énergie rayonné. Ce flux peut être converti en nombre de photons grâce à la
constante de Planck qui lie la fréquence d'un photon à son énergie. Lorsqu'on
tient compte de tous les facteurs géométriques et des correspondances entre les
unités, le nombre N.Dn de photons pour un intervalle de
fréquence Dn est![]() , où L est la longueur dans le milieu transparent
souvent appelée radiateur, Z le nombre de
charges élémentaires possédées par la particule, et a la constante de
structure fine (
, où L est la longueur dans le milieu transparent
souvent appelée radiateur, Z le nombre de
charges élémentaires possédées par la particule, et a la constante de
structure fine (![]() ) et h la constante de Planck.
) et h la constante de Planck.
Lumière Tcherenkov et
astrophysique. Avec l'avènement des satellites et des nouveaux moyens de détection au
sol, les astronomes ont accru considérablement leur possibilité d'observation
en détectant des photons d'énergie de plus en plus haute. On est passé grâce
aux satellites de la lumière ultraviolette (10 eV) aux rayons X
(103 eV) puis aux rayons g de l'ordre du gigaélectronvolt. Plusieurs
sources ponctuelles de rayons g ont été découvertes. Certaines sont des
galaxies à noyau actif, d'autres sont des étoiles à neutrons ou pulsars. Les
galaxies avec un noyau actif semblent émettre des rayons g de toutes
énergies; leur mécanisme de production n'est toujours pas compris. Les étoiles
à neutrons, qui sont très compactes, tournent extrêmement vite (1
000 tours par seconde) et sont le siège de champs électrique et magnétique
gigantesques permettant d'accélérer des particules à des énergies phénoménales
(100 TeV; 1 TeV = 1012 eV). Dans ces deux cas, il est très
intéressant de mesurer les rayons g du cosmos au-delà de 100 GeV, ne
serait-ce que pour comprendre la raison de ces émissions. Ces énergies sont
inaccessibles aux satellites, car elles nécessitent des masses considérables
pour les détecter et les mesurer. En revanche, grâce à la lumière Tcherenkov,
ces rayons g sont détectables et mesurables avec des détecteurs au sol:
les rayons g de l'ordre du téraélectronvolt génèrent dans la haute
atmosphère une gerbe d'électrons positons qui se propage jusqu'au sol. Ces
électrons ou positons sont tous hautement relativistes et restent dans
l'alignement du g initial. Ils émettent de la lumière Tcherenkov vers le sol.
Cette lumière est importante. Un g de 1 TeV envoie au sol environ 3106
photons dans le visible répartis sur un cercle de 120 mètres de rayon. Le
nombre de ces photons est proportionnel à l'énergie du rayon g. Avant de
toucher le sol, ils sont répartis sur la surface du cône Tcherenkov. Ce cône a
la forme d'un parapluie largement ouvert de 1 mètre d'épaisseur et de
120 mètres de rayon. Son manche serait dans la direction du g initial, et
donc aussi dans la direction de l'étoile ou de la galaxie source. La lumière
Tcherenkov est collectée par un ou plusieurs miroirs vers des détecteurs
(photomultiplicateurs) capables de mesurer de très faibles intensités
lumineuses produites durant des temps extrêmement brefs (10 nanosecondes,
10-8 s). La brièveté est capitale, car elle permet de distinguer la
lumière Tcherenkov de toutes les autres sources lumineuses qui sont
généralement continues. Certaines expériences utilisent un très grand miroir de
collection (75 m2 pour le détecteur du mont Hopkins en Arizona. D'autres
éparpillent les collecteurs de lumière (18 miroirs de 0,5 m2 pour
l'expérience Thémistocle à Targasonne, dans les Pyrénées) qui analysent le cône
Tcherenkov plus en détail. Ces deux types d'expériences déterminent la
direction de la gerbe par la forme du cône Tcherenkov et son énergie par le
nombre de photons collectés. Un grand miroir peut se contenter d'un nombre plus
réduit de photons pour identifier un g; son seuil d'énergie est de 300 GeV
environ. Les expériences utilisant de nombreux détecteurs dispersés nécessitent
au moins 3 TeV (3 ´ 1012 eV) pour faire une détection, mais sont plus
précis dans la mesure de l'énergie et de la direction.
9. L’expérience de STERN & GERLACH
(à suivre !)
10. L’effet CASIMIR (1948)
L’effet Casimir se manifeste sous
la forme d’une force attractive très faible entre deux plaques métalliques
extrêmement proches situées dans une cavité vide résonnante (boîte métallique
hermétiquement fermée) en absence de champ électromagnétique.

Selon la théorie classique
de l’électromagnétisme et la mécanique classique, les deux plaques devraient
rester immobiles puisqu’il règne dans la cavité un vide absolu de tout champ,
et par conséquent aucune force n’agit sur les plaques (à part la force de
gravitation sui attire tous les corps entre eux, mais celle –ci est extèmement
faible). Pour pouvoir se mouvoir, les plaques métalliques ont besoin d’énergie
qu’elles ne peuvent puiser nulle part.
L’effet Casimir est un
pur résultat de la théorie quantique des champs. Il a été imaginé et calculé
par le physicien hollandais Hendrick
Casimir en 1948.
Selon la théorie quantique des champs, le champ
électromagnétique (et ceci est d’ailleurs applicable à tous les champs
quantiques) possède des états d’énergie différents. L’état de plus basse
énergie - l’état fondamental -
correspond à l’absence de quanta d’énergie (les photons dans le cas du champ
électromagnétique) ou en d’autres termes, le vide. Le premier état « excité »
est l’état à un quantum d’énergie ou à un photon. Le second état excité est
l’état à deux photons, et ainsi de suite.
Cependant, la
représentation que donne la théorie quantique des champs du vide est pour le
moins paradoxale. Ce vide est en fait bourré d’énergie qui n’est pas «
matérialisée » sous forme de particules. Toutefois, sur de courtes durées,
cette énergie peut se matérialiser en particules ou quanta dont la durée de vie
est très brève. On les appelle des particules virtuelles. Quoique étant
qualifiées de virtuelles, les effets de ces quanta (des photons dans notre cas)
sont bel et bien réels.
Dans la cavité, des
quanta virtuels (des photons virtuels) vont donc spontanément « émerger » du
vide. Le spectre des longueurs d’onde de ces photons est continu mais du fait
que la cavité est fermée, la plupart des fréquences vont être destructives et
finalement seules quelques fréquences particulières (appelés modes de résonance) vont subsister dans la cavité suite à l’apparition en
régime stationnaire d’ondes stationnaires. C’est là le phénomène classique de
résonance dans une cavité résonante. Les modes de résonance
sont caractérisés par le fait que la longueur d’onde du mode est un
sous-multiple entier de la distance qui sépare les faces de la cavité. Le
nombre de modes autorisés est donc proportionnel à la distance qui sépare les
faces de la cavité.

Dans la configuration qui nous intéresse, il s’établit des résonances entre
les faces de la cavité et les plaques et entre les plaques elles-mêmes. Si la
distance entre les plaques est inférieure à leur distance avec les faces de la
cavité, alors il existera davantage de modes de résonance entre les faces de la
cavité et les plaques, qu’entre les plaques elles-mêmes. La pression de
radiation qui s’exerce sur les faces "internes" des plaques est donc
inférieure à celle qui s’applique sur leurs faces "externes". Il en
résulte une force très faible qui rapproche les plaques l’une vers l’autre.

Bien que prédit depuis
1948, cet effet n'a été observé expérimentalement pour la première fois qu'en
1997. Pour être rigoureux, il faudrait faire intervenir les quanta de tous les
champs quantiques existants. Mais ces champs requièrent beaucoup d’énergie pour
se matérialiser à partir du vide ce qui se traduit par une faible probabilité
de matérialisation des quanta associés comparativement au champ
électromagnétique. Par conséquent, leur contribution à l’effet Casimir est très
largement négligeable.
L'effet Casimir montre
qu'avec du vide, il est possible de générer du mouvement. En cela il constitue
une violation majeure du principe
classique de conservation de l'énergie et permet de mesurer combien la
physique quantique peut être déroutante!
11. L’effet STARK
Sous l’action d’un champ électrique, les niveaux d’énergie
d’un atome sont perturbés, et par conséquent, les raies émises par cet atome
seront modifiées. Elles sont composées en plusieurs raies dont la "raie
moyenne" peut être déplacée par rapport à la raie initiale. Cet effet, qui
est analogue à l’effet ZEEMAN, est cependant beaucoup plus complexe à
observer, car une source lumineuse est le plus souvent composée d’un gaz
partiellement ionisé dans lequel le champ électrique qu’on peut appliquer est
limité par la conductivité.
C’est en 1913 que J. STARK et A. LO SURDO
purent mettre en évidence cet effet séparément. LO SORDO qui utilisait
le même champ électrique pour créer la décharge et l’effet, ne pouvait faire
que des études quantitatives. STARK utilisait 2 champs différents, et
les ions excités dans la décharge passaient entre deux électrodes fournissant
le champ perturbateur. Actuellement, l’étude de l’effet STARK se fait avec le
calcul des perturbations, et on montre que la décomposition des niveaux se fait
avec levée de dégénérescence sur le nombre quantique ml et
que l’écart entre la raie initiale et le niveau perturbé peut s’écrire : DW = aE +bE² +cE3 + …où E est le coefficient
du champ électrique et les coefficients a, b, c, … des coefficients dépendant
des nombres quantiques.
Un cas particulier est celui des ions hydrogénoïdes où a est prépondérant par rapport aux
autres, ce qui fait que la dépendance devient linéaire. Pour la raie de BALMER
par exemple, pour une longueur d’onde de 486 nm et un champ d’intensité 100
000V/cm, la séparation entre les composantes extrêmes sera de 3 nm. Pour
des atomes à 2 électrons optiques ou plus, l’effet STARK est quadratique
(proportionnel au carré du champ électrique), et il apparaît alors un décalage
vers le bleu ou le rouge suivant les raies.
Cet effet est important en physique des plasmas, car les
atomes émetteurs sont dans le champ créé par l’ensemble des ions et des
électrons environnants. Ce champ est variable dans le temps et dans l’espace
(évolution du plasma et micro-instabilités), et on observe souvent un profil
"moyen". Cependant, on peut arriver à calculer à partir de ce profil
moyen, ma répartition du champ électrique, et par conséquent, la densité
électronique dans le plasma. Cette méthode, bien qu’approximative, reste quand
même utilisée dans les cas où le plasma est inatteignable (dans l’espace par
exemple) ou alors qu’on ne veut pas le perturber.
12. L’effet tunnel
(à suivre !)
13. L’effet DOPPLER
(à suivre !)