Chapitre IV : Quelques notions de physique
quantique __________________________________________________
table des matières de la page :
2. L'équation d'onde de
Schrödinger
3. Les quatre nombres
quantiques
9. Le principe d’incertitude
de Heisenberg (1927)
10. Les classes d’équivalence
d’histoires
__________________________________________________
1. La dualité onde-corpuscule
Que les atomes soient
constitués de particules, soit, mais il restait encore des phénomènes
inexplicables. Comme les ondes électromagnétiques ont des caractéristiques de
particules, le physicien français De
BROGLIE Louis Victor suggère, en 1924, que les particules
pourraient aussi, dans certains cas, montrer des propriétés d'ondes. Quelques
années plus tard, cette prédiction fut vérifiée expérimentalement par les
physiciens américains DAVISSON Joseph, GERMER Lester Halbert et le Britannique THOMSON George Paget. Ils montrèrent qu'un faisceau
d'électrons dispersés par un cristal génère une diffraction caractéristique
d'une onde.
2. L'équation d'onde de Schrödinger
La notion ondulatoire de
la particule permet au physicien australien Schrödinger Erwin de développer une
équation dite équation
d'onde pour décrire les propriétés ondulatoires de
la particule et, plus particulièrement, le comportement de l'électron dans
l'atome d'hydrogène :
L'équation d'onde de Schrödinger présente quelques solutions
discrètes seulement, ces solutions sont des expressions mathématiques dont les
paramètres représentent les nombres quantiques. (Les nombres quantiques sont
des entiers introduits dans la physique des particules pour exprimer la
grandeur de certaines quantités caractéristiques des particules ou des
systèmes). Les solutions de l'équation de Schrödinger indiquent aussi que les quatre nombres quantiques
de deux électrons ne peuvent pas occuper le même état énergétique. Cette règle,
déjà établie empiriquement par le physicien suisse PAULI Wolfgang, en 1925, est appelée principe d'exclusion.
3. Les quatre nombres quantiques
a) Le premier : n, le nombre quantique principal
Il ne peut prendre que
des valeurs strictement positives : 1,2,3,…Dans le cas des atomes
hydrogénoïdes,
l’énergie ne dépend que de ce
nombre quantique : 
.
b) Le second : l, le nombre quantique orbital
Il est lié au module du moment cinétique orbital de
l’électron comme l’a postulé Bohr : 
.
Il est compris entre 0 et (n-1).
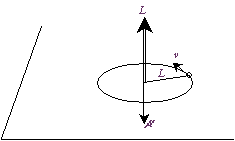
c) Le troisième : ml, le nombre quantique magnétique
Il représente les valeurs des projections possibles du moment cinétique orbital sur un axe donné.
Il ne
peut prendre que 2l+1 valeurs (règle de Slater) allant de –l à +l.
Remarque : non seulement la
longueur de ce moment est quantifiée, mais sa projection sur un axe disons
z l’est aussi : 
.
d) Le quatrième : s, le spin
4. La superposition d’état
Voila encore une exclusivité
quantique. Le principe de superposition affirme que les caractéristiques d'un
atome, d'une particule ou d'un système quantique en général constituent un
état. Or, quand un système à plusieurs état possibles, la somme de tous ces
états est également un état possible! Le système se trouve alors dans une
superposition d'état. C'est grâce à ce principe qu'une particule peut occuper
plusieurs positions à la fois ou qu'un atome peut se trouver dans un état de
superposition d'énergies. Ce phénomène est bien sur impensable dans l'univers
classique. Le simple fait de mesurer fait disparaître la superposition d'état
au profit d'un seul. Pourtant à défaut d'avoir une mesure de la superposition
d'états la théorie quantique nous donne la probabilité qu'on a de mesurer
chaque état.
Remarque: Pour rester dans le
domaine de la cosmologie, on peut souligner une hypothèse intéressante de EVEREST Hugh qui postule qu’à
chaque réduction du nombre d'états il n'y a pas passage de superposition d'états
à un seul mais réalisation de tous les état dans un univers différent. Théorie
qui reste, à priori, invérifiable de par le fait que les univers parallèles ne
communiquent pas entre eux.
8. La théorie des quarks
La théorie des quarks est
intéressante à plusieurs titres. D'abord elle fournit un modèle cohérent et
fiable de l'interaction forte en bon accord avec l'expérience. Ensuite, elle
constitue une illustration simple de l'application des théories de jauge.
Dans les années soixante,
les physiciens avaient accumulé beaucoup de données expérimentales sur le
comportement des particules élémentaires. Les progrès réalisés dans la
technologie des accélérateurs de particules permirent d'atteindre des énergies
élevées. Ceci eut pour conséquence immédiate l'observation d'une multitude de
nouvelles particules (des centaines) dont certaines avaient une durée de vie
très brève (10-24 s). Cette profusion de particules incita les
physiciens de l'époque à abandonner le qualificatif élémentaire pour décrire le monde des particules. Dans un souci de
simplification, ils entreprirent la synthèse des résultats expérimentaux
obtenus. Les observations tendaient à montrer l'existence d'une structure plus
fine des particules sensibles à l'interaction forte (famille de particules
baptisée hadrons). Trois propriétés se détachèrent des informations
recueillies :
1.
un nombre purement abstrait, le
nombre baryonique qui dénombre les baryons impliqués dans une interaction, est une quantité
conservée durant l'interaction,
2.
les particules ayant une durée de vie très courte ressemblent à des états
liés instables de particules sous-jacentes. Un peu à la manière des noyaux
atomiques instables, elles se désintègrent après une durée de vie très courte,
3.
les expériences à haute énergie ont mis en évidence des comportements qui
ne peuvent être pleinement expliqués qu'en émettant l'hypothèse de
sous-constituants (observation de jets de particules).
L'ensemble de ces faits
donnèrent naissance à la théorie des quarks, selon laquelle, les hadrons
(particules sensibles à l'interaction forte) seraient composés d'autres
particules plus fondamentales : les quarks.
D'après cette théorie,
les quarks possèdent une propriété unique dans la nature : leur charge
électrique est fractionnaire (
e ou 
e où e est la charge de l'électron). Or, aucune expérience
n'a pu mettre en évidence, pour l'instant, l'existence de charges
fractionnaires. Cela signifie, qu'un quark ne peut exister à l'état isolé. Il
est forcément lié à d'autres quarks dans un hadron de façon à ce que la charge
électrique totale soit nulle ou égale à un multiple entier de e. Aux niveaux
d'énergie auxquels les accélérateurs de particules travaillent aujourd'hui, il
semble impossible de pouvoir isoler un quark. Cette propriété est connue sous
le nom de confinement des quarks dans les hadrons.
Le tableau suivant donne
un aperçu des principales caractéristiques des quarks.
|
|
u (up) |
d (down) |
s (strange) |
c (charm) |
b (bottom) |
t (top) |
|
Charge
électrique |
2/3 |
-1/3 |
-1/3 |
2/3 |
-1/3 |
2/3 |
|
Masse |
2 à 8 MeV |
5 à 15 MeV |
100 à 300 MeV |
1 à 1,6 GeV |
4,1 à 4,5 GeV |
170 MeV |
|
Spin |
½ |
½ |
½ |
½ |
½ |
½ |
Les principaux hadrons
connus sont composés des combinaisons de quarks suivantes :
|
Hadrons |
Composition en quarks |
|
Proton |
u, u, d |
|
Neutron |
u, d, d |
|
p+ |
u, anti-d |
|
p- |
d, anti-u |
|
p0 |
u, anti-u ou d, anti-d |
|
K+ |
u, anti-s |
|
K- |
anti-u, s |
|
K0 |
d, anti-s |
|
f |
s, anti-s |
A partir de ces données,
les physiciens ont développé un modèle pour les quarks et l'interaction forte.
L'équivalent de la charge électrique pour l'interaction forte a été baptisé la "couleur". Il va de soi que cette
couleur dont il est question ici n'a rien à voir avec la couleur des objets. En
fait, il s'agit d'une grandeur abstraite qui peut prendre 3 valeurs distinctes
: les trois couleurs fondamentales (rouge, bleu, jaune) et les anti-quarks
pouvant avoir les trois couleurs complémentaires à ces couleurs fondamentales.
Le principe étant qu'un hadron est toujours neutre du point de vue de
l'interaction forte c'est-à-dire que la somme des "couleurs" de tous
les quarks contenus dans le hadron est blanche.
Il existe deux façons
d'obtenir du blanc :
1.
en ajoutant les 3 couleurs fondamentales ou leurs couleurs complémentaires,
2.
en ajoutant une couleur et sa couleur complémentaire
Ainsi, il existe deux
sortes de hadrons : des hadrons à trois quarks de couleur différente (couleurs
fondamentales ou couleurs complémentaires aux couleurs fondamentales), des
hadrons à deux quarks ayant chacun la couleur complémentaire à l'autre. C'est
en effet ce qui est observé dans la nature. Le premier type de hadrons forme la
famille des baryons (qui veut dire lourd en
grec) et le second type constitue la famille des mésons (milieu en grec).
Le champ de force liant
les quarks entre eux est la force forte. Les quanta de cette interaction
s'appellent les gluons (de "glue" qui
signifie "colle" en anglais). A la différence du quantum de
l'interaction électromagnétique - le photon - qui n'est pas chargé, les gluons
ont deux charges fortes, c'est-à-dire deux couleurs. Si l'on combine par paires
l'ensemble des couleurs et des couleurs complémentaires (que l'on nomme aussi anti-couleurs) l'on obtient 8 combinaisons possibles ce qui nous donne donc 8 gluons.
La formulation théorique
de la théorie des quarks a très vite adopté celle d'une théorie de jauge. La
théorie porte le nom de chromodynamique
quantique (Quantum chromodynamics
en anglais ou QCD). Comme nous
l'avons dit, les hadrons doivent toujours être "blancs". Si l'on
permute les couleurs des quarks contenus dans un hadron, le résultat final n'a
pas changé : le hadron est toujours de même nature et reste "blanc".
Cette opération de permutation met donc en évidence l'invariance de
l'interaction forte par permutation des couleurs des quarks. Si l'on permute
partout dans l'univers les couleurs des quarks, alors les phénomènes impliquant
l'interaction forte restent inchangés. La permutation de tous les quarks dans
l'univers est une transformation globale.
Forts de cette symétrie
globale, les physiciens ont imposé à l'interaction forte d'être de plus
symétrique (ou invariante) pour des transformations "locales" -
c'est-à-dire ponctuelles - de couleur des quarks. En d'autres mots, les lois de
l'interaction forte doivent rester identiques si l'on change la couleur de
quelques quarks pris isolément. Prenons le cas d'un proton (composition en
quarks = uud). Initialement il contient un quark u rouge, un quark u bleu et un
quark d jaune; il est donc "blanc". Si l'on permute la couleur de
tous les quarks du proton, il conserve sa couleur "blanche" et reste
un proton (les quarks n'ont pas changé et sont toujours uud) . En revanche, si
l'on modifie de façon arbitraire la couleur d'un seul quark, la couleur totale
du hadron ne sera plus "blanche". L'une des principales règles qui
régit les interactions fortes est donc violée, ce qui revient à dire que,
naturellement, l'interaction forte n'est pas symétrique pour des
transformations ponctuelles et arbitraires de couleur des quarks (pas de
symétrie locale). En imposant l'invariance locale, il apparaît alors dans les
équations un terme qui vient compenser la modification de la couleur du quark
en provoquant le changement de couleur d'un autre quark du proton de manière à
ce que ce dernier reste "blanc". Ce terme compensateur n'est rien
d'autre qu'un champ dont les quanta sont, comme vous l'aurez deviné, des
gluons.
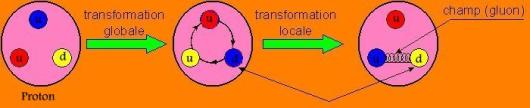
Ainsi le champ de gluons
prend-il sa source dans la symétrie de l'interaction forte vis-à-vis du
changement de couleur des quarks.
D'un point de vue
mathématique, on peut représenter la couleur d'un quark par une flèche qui
s'oriente selon un axe dans un espace qui en compte trois : un axe bleu, un axe
rouge et un axe jaune (les trois couleurs possibles d'un quark). La
modification de la couleur d'un quark consiste à faire tourner la flèche dans
cet espace à trois dimensions de manière à l'aligner avec l'axe de la nouvelle
couleur. Cette opération revient donc à faire une rotation dans un espace à
trois dimensions.
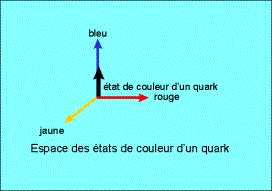
Figure 1 : les couleurs d'un quark
Les rotations que nous
avons décrites ne s'appliquent pas sur des vecteurs mais sur des êtres
mathématiques plus complexes : les spineurs. L'ensemble de ces rotations forme un groupe nommé SU(3) (Symétrique Unitaire 3). Tout comme dans le cas de la QED, on
se réfère souvent à la théorie des quarks ou QCD par le groupe qui représente
l'interaction électromagnétique, c'est-à-dire par le nom de SU(3).
8. La théorie des quanta
Le premier développement
qui conduisit à la résolution des difficultés théoriques que les observations
amenaient fut l'introduction par le physicien allemand Max Planck de la notion de quantum comme réponse aux
études conduites par les physiciens sur le rayonnement du corps noir, pendant
les dernières années du XIXe siècle. Planck utilisa l’idée des
quanta pour expliquer pourquoi un morceau de métal chauffé au rouge n’émet pas
une quantité infinie de chaleur ; mais il considérait les quanta comme un pur artifice théorique
sans aucun rapport avec la réalité physique. Son idée était que l'énergie était
rayonnée seulement par quanta d'énergie e=hn, où n est la fréquence et h le
quantum d'action, connu aujourd'hui sous le nom de constante de Planck. En
1900, Planck affirma donc que la
matière ainsi que l'énergie rayonnante ont une structure discontinue et postula
que la matière ne peut émettre ou absorber l'énergie rayonnante que par petites
unités discrètes appelées quanta.
En 1905, la même année que
celle où il publie son article sur la relativité restreinte, Einstein publie un
article consacré à l’effet photoélectrique. On avait observé que lorsque la
lumière tombait sur certains métaux, il se produisait une émission de
particules chargées. Cependant, quand l’intensité de la lumière envoyée
diminuait, le nombre de particules mises diminuait également, mais la vitesse
d’émission restait constante. Einstein montra que cela ne pouvait s’expliquer
que si la lumière arrivait non pas par quantités continûment variables, mais
seulement par paquets d’une certaine dimension : en effet chaque particule
émise correspondait à un quanta de lumière venait frapper le métal.
Mais ce ne fut qu’en 1924
que l’on a compris réellement toutes les implications de l’effet photoélectrique,
lorsque Werner HEISENBERG a fait remarquer que cela signifiait qu’il est
impossible de mesurer exactement la position d’une particule.
9. Le principe d’incertitude de Heisenberg (1927)
En effet, pour regarder
un objet, il faut envoyer de la lumière dessus. Or Einstein avait montré que la
quantité minimale de lumière était un quanta. Or ce quanta ayant une certaine
énergie et percutant la particule, il va donc lui conférer un surplus d’énergie
et/ou de vitesse : les mesures seront donc faussées ! Plus on cherche
une mesure exacte, plus l’énergie du paquet
de lumière à utiliser doit être grande et par conséquent plus la
perturbation sera grande et les mesures imprécises. Cette impossibilité de localiser
une particule avec exactitude à un moment précis a été analysée par Werner Heisenberg qui, en 1927, formule le principe d'incertitude suivant :
et 
les trois premières
relations traduisent ce que nous venons de dire : quelque soit la façon
dont on s’y prend pour les mesures, l’incertitude sur sa position multipliée
par celle sur sa vitesse restera toujours supérieure à une certaine quantité
minimale, appelée constante de Planck et notée 
.L’impossibilité de déterminer exactement l’énergie d’une
particule si le temps de mesure est trop court. Cette dernière relation permet
aussi de comprendre ce que sont les particules virtuelles : en vertu de ce principe, l’énergie d’une
particule peut fluctuer au tour de sa valeur « moyenne » de DE, pendant une durée moyenne Dt. Pendant cet intervalle de temps
vont être formées des paires de particules dites virtuelles qui vont avoir pour
énergie DE. Lorsque cette énergie
devra être restituée, ces paires vont s’annihiler paire par paire en redonnant
l’énergie qui leur avait été attribuée. Ceci n’est pas du à l'imprécision des
appareils de mesure, mais à une caractéristique intrinsèque du monde quantique.
En premier lieu, il est impossible de mesurer la position d'une particule sans
perturber sa vitesse. Les connaissances de la position et de la vitesse sont
dites complémentaires, c'est-à-dire qu'elles ne peuvent pas être précisées
simultanément. Ce principe est aussi fondamental si l'on veut comprendre la mécanique quantique telle qu'elle est
conçue aujourd'hui: les caractères ondulatoire et corpusculaire du rayonnement
électromagnétique peuvent être compris comme deux propriétés complémentaires du
rayonnement.
Une des implications de
ce principe est que si on est incapable de savoir où est la particule dans le
présent, on est incapable de prédire son avenir. Le mieux que l’on puisse faire
est de donner les différentes probabilités de chacune des issues. Le physicien
américain Richard FEYMAN a trouvé une manière élégante d’éviter ces
paradoxes qui préoccupaient Einstein. Connu pour ses célèbres diagrammes qui
portent son nom, son concept de somme sur les histoires fut plus important
encore, comme nous allons le voir.
10. Les classes d’équivalence d’histoires
Que signifie faire l’analyse des classes d’équivalence des histoires
possibles de l’Univers comme le disent les mathématiciens ?
Le but est de savoir, parmi les différentes classes d’équivalences
d’histoires possibles, disons les différentes histoires de l’Univers pour
simplifier, quelle est la probabilité que l’une ou l’autre séquence ait lieu.
En d’autres termes, si A et B sont deux évolutions possibles de l’Univers, la
probabilité que l’une des deux histoires se réalise est la probabilité de A
plus la probabilité de B.
Les résultats possibles sont mutuellement exclusifs et toujours exhaustifs
: un seul univers doit émerger et le résultat doit se produire. Comme au
tiercé, tous les turfistes attendent un résultat et un seul cheval doit gagné.
C’est la même chose dans l’approche probabiliste des conditions d’émergence de
l’Univers.
D’un autre côté, on ne peut attribuer de probabilité, en général, qu’à des
paires d’histoires de l’Univers. Si de plus, les histoires interfèrent entre
elles, on ne peut plus calculer leur probabilité.
Pratiquement, une histoire présente une séquence d’événements complets.
Mais il est impossible, en vertu du principe d’incertitude, de préciser la
position et la quantité de mouvement de toutes les entités de l’Univers, ni
même de l’une d’entre elle. Nous devrons donc être plus sélectifs. Cette
contrainte nous permet déjà de dire qu’une éventuelle théorie “de Tout” ne
pourra jamais englober tous les phénomènes. Nous y reviendrons.
Une classe d’histoires ne représente que les ensembles d’histoires qui
partagent les mêmes éventualités possibles, par exemple, la détermination
exacte de la position de tous les corps qui peuplent l’Univers.
Mais faut-il pour cela déterminer tous les instants pour chaque entité, et
à ces instants considérer les interactions avec tous les corps de l’Univers ?
On peut en effet ne considérer que les entités qui conduisent à l’univers
“gagnant” et ignorer certains événements non significatifs (qui seront
sursommés dans l’opération de sommation).
Deux classes d’histoires de ce type forment ce que les mathématiciens
appellent des classes d’équivalences d’histoires ou “coarse grain stories”, qui
donna le néologisme agraidissement.
Pour déterminer la probabilité de trouver l'univers dans un état
particulier à partir d'un état antérieur, nous devons donc calculer son
histoire idéale à partir de toutes les classes d’histoires théoriquement
possible de l'espace et du temps. C'est que l'on appelle la "fonction de
transition".
Ce calcul revient à effectuer un “survol”, c’est-à-dire voler en ignorant
les détails du terrain.
Ainsi dans la prédiction du mouvement des planètes du système solaire, on
représente les planètes par leur seul centre de masse ponctuel. Les dimensions
du système se voient ainsi réduites drastiquement.
On élude ainsi les histoires non significatives car la somme de toutes les
interférences positives ou négatives qui ont lieu entre paires d’histoires ne
laissent qu’une petite probabilité d’existence, positive, négative, voire
nulle. Si la valeur est nulle, toutes les histoires décohèrent, c’est-à-dire
qu’elles donnent lieu à de véritables probabilités. Ainsi quand le photon
interfère avec lui-même dans l’expérience des deux fentes de Young,
l’interférence des deux histoires ne permet pas de lui assigner de probabilité.
Et la question de savoir par quelle fente est passé l’électron n’a donc plus de
sens, comme si “le cheval n’avait plus de cote” ainsi que le dit Murray
Gell-Mann.
Calculer l'intégrale de ces classes d'histoire équivaut donc à calculer une
fonction d'onde sommée sur une certaine classe d'histoires du système. Les
histoires se matérialisent (se réduisent) au moment où l'on connaît la valeur
de la fonction d'onde. Celle-ci étant unique on peut alors remonter le temps et
déterminer la classe d'histoires qui doit être sommée. De cette façon, les
nombres complexes associés aux histoires de l'Univers sont définis par les
seules lois de la physique.
La particularité de cette méthode complexe d'intégration est de tenir
compte, rappelons-le, de toutes les histoires possibles contenues dans le
système. Calculer cette intégrale équivaut à résoudre l'équation de
Schrödinger. C'est une solution quantifiée qui généralise son application à
l'Univers tout entier. Car résoudre l'intégrale des histoires du système
équivaut bien à résoudre l'équation de Wheeler-De Witt. Bien sûr la précision de
cette solution dépend du nombre et du choix des classes d'histoires que l'on
somme. Hartle et Hawking suggèrent que cette solution n'est possible que si
l'on considère l'intégrale de toutes les géométries de l'espace-temps qui n'ont
pas de limites, mis à part le temps présent qui reste ouvert et sans frontières
définies.
Le fait qu'il y ait une singularité dans le modèle classique ne permet pas
de résoudre cette équation. La mécanique quantique permet d'y voir plus clair
en ce sens que la méthode de sommation d'une classe d'histoires du système
accepte plusieurs histoires et pas uniquement celles prévues par la physique
classique. Plutôt que de tomber dans une singularité initiale, ce modèle permet
à l'Univers de se "recourber" graduellement telle une surface
hémisphérique plutôt que de former un cône de plus en plus étroit. Cet
espace-temps se détermine dans un temps imaginaire qui ne contredit pas le
théorème de la singularité classique. Par contre, si ces histoires contiennent
des singularités, les lois de la physique ne permettraient pas de déterminer
leur probabilité, et il s'agirait de conditions initiales instaurées par un
facteur extérieur, tel que Dieu.
C'est ainsi que la solution de l'équation de Wheeler-De Witt permet à
l'Univers sans bord de devenir ce qu'il est à partir de rien. En fait il obéit
à son tour à l'effet tunnel mais dont le développement est en quelque sorte
inversé. Du fait qu'il s'agit d'une fonction d'onde sans limite, l'Univers a
une forte probabilité d'obéir aux lois classiques - grande taille et faible
densité – plutôt que d'obéir à l'effet tunnel ordinaire dans lequel il n'existe
pas de transition de la dimension zéro à la grande taille, où l'Univers a toute
les chances de rester confiné et de contenir une densité d'énergie très élevée.
Maintenant résumons-nous. A la condition que l'Univers n'ait pas de limite
- sans bord - et en tenant compte de l'effet tunnel, la fonction d'onde unique
de l'Univers a pu apparaître spontanément dans le vide quantique. Ce modèle
obéit à la cosmologie classique dès qu'il a franchit le seuil des 10-33 cm environ, ce qui est en parfait accord avec les observations. En deçà de
cette dimension, la fonction d'onde indique que l'espace-temps classique
n'existe pas.
Le point fort du modèle d'univers sans bord proposé par Hartle et Hawking[1] en 1983
est d'éliminer les fluctuations de densité du champ scalaire originel (champ
d'énergie d'intensités variables). Ces inhomogénéités émergent naturellement
pourrait-on dire de la théorie quantique.
L'état d'énergie de la singularité imaginaire est tout à fait exempt de
fluctuations et reste régulier.
C'est en évoluant dans le temps imaginaire que les fluctuations quantiques s'amplifient
et pointent le jour dans une région réelle qui sera notre bulle-univers. Cette
région est réduite à la taille minimale prédite par le modèle inflationnaire.
Si l'Univers est bel et bien issu d'une seule fonction d'onde, nous pouvons
alors nous demander comment l'Univers a-t-il commencé ? A partir de l'idée
émise par Tryon, A.Guth et E.Farhi[2] proposèrent
en 1987 de vérifier son hypothèse en laboratoire. Leur scénario se base sur le
fait que l'Univers aurait émergé ayant déjà une taille non nulle et fermé, sa
densité d'énergie étant réglée par une sorte de flou quantique dans laquelle la
théorie de la relativité générale d'Einstein s’évanouit. Ils proposèrent une
expérience dans laquelle le rayonnement serait confiné jusqu'à une densité
d'énergie inouïe de 1075 gr/cm3,
la densité d'un trou noir.
Guth et Farhi prédisent que lorsque cet "Univers-éprouvette"
sera animé d'une certaine vitesse d'expansion, il s'effondrera selon les lois
de la physique quantique. Mais au lieu de former une singularité, l'effet
tunnel provoquera sa détente et donnera naissance à une bulle d'Univers en
expansion. L'exercice de style est alléchant. Nous ignorons cependant comment
était l'Univers primordial. Nous ignorons si les particules virtuelles d'alors
baignaient dans un vide quantique comme elles y sont plongées actuellement
(probablement pas), tout comme il nous est actuellement impossible de savoir
quelle était l'influence de la gravitation dans un Univers naissant exempt de
toute matière.
Si Guth et ses collègues théoriciens parvenaient à créer spontanément cet
Univers-éprouvette ils devront également expliquer la formation des structures
cosmiques à partir de l'inflation...
Ces problèmes ne peuvent être résolus que par les physiciens les plus
géniaux, ceux passant leurs journées derrière leur ordinateur ou craie en main
sur les tableaux noirs de l’université de Cambridge, Phi Bêta Kappa, Berkeley,
du MIT ou du CERN. Car comme l'a très bien dit Hawking, la physique moderne
bute sur les singularités. Si nous voulons résoudre ces difficultés, nous
devrons modifier la théorie de la relativité générale qui dans l'état actuel de
nos connaissances est une théorie incomplète. Imaginer que ces équations
doivent rendre compte de l'état actuel de l'Univers, sa platitude apparente et
son homogénéité à grande échelle à partir d'une fluctuation quantique qui
survint en l'espace de 10-32 sec ! On ne peut que
saluer bien bas ces physiciens qui tentent de découvrir cette "équation de
l'Univers".
Les rationnels expliquent les choses autrement, jugeant la théorie d'Alan
Guth fort extravagante. Le modèle inflationnaire disent-ils, est parfait mais
il cache une seule contrainte, les
physiciens attendent que Guth et Farhi inventent le laboratoire qui permettrait
de vérifier cette expérience ! Car où sont les preuves de tout cela ? Les
physiciens peuvent déjà comparer leurs prédictions quantiques avec les
conditions initiales imposées par les modèles classiques.
Si le succès sourit à certains chercheurs, leurs preuves sont toutefois
indirectes. Les observations seraient une preuve irréfutable. L'évolution de
l'Univers ayant balayé quasiment toute trace de son passé, seules restent les
hypothétiques ondes gravitationnelles qui se sont propagées dans tout l'espace
sans pratiquement interagir avec la matière. Mais leur détection est très
difficile et nous arrivons à peine à construire les détecteurs qui
permettraient de les déceler. En fait si nous les découvrons un jour, leur
spectre nous révélera la lumière de la création.
Si on parvient un jour à découvrir une théorie unifiée, si on peut calculer
la condition initiale, Gell-Mann11 nous dit que “les lois
fondamentales de la physique et celles des particules élémentaires [deviendront
] une seule et même loi”. Mais ajoute-t-il de suite,
étant donné qu’il s’agit de lois quantiques non déterministes, les prédictions
que l’on pourra établir ne seront jamais que des probabilités. C’est en ce sens
que la théorie “de Tout” sera une approximation.
Malheureusement les probabilités n’ont pas bonne presse. S’il nous est déjà
impossible de mesurer l’instant de démarrage d’un laser ou l’instant de
désintégration d’un atome radioactif, penser à la difficulté de prédire
l’avenir de l’Univers...
Car malgré nos lois fondamentales, la complexité de l’Univers ne peut
satisfaire une description algorithmique comme Chaikin, Wheeler ou De Witt ont
essayé de le faire.
Trop d’événements relèvent du hasard ou de conditions initiales survenues
il y 5, 10 ou 20 milliards d’années dont les conséquences à long terme sont aussi
considérables qu’imprévisibles. Pauvre éphémère que nous sommes dont
l’existence même introduit une dépendance sensitive de l’avenir aux conditions
initiales...
Quoi qu'il en soit la cosmologie quantique nous a permis de comprendre
certaines questions fondamentales concernant l'origine de l'Univers et de
formuler le sens de certaines propositions.
Il est de notre intérêt
de bien comprendre ces concepts pour pouvoir répondre à l'ultime question :
Pourquoi l'Univers?