CHAPITRE III : LES DIFFERENTES THEORIES DES CORDES

Avant de commencer à dire quelques mots de ce qui semble être une des expériences les plus excitantes de la physique contemporaine, je voudrais insister sur un point qui ne m’avait pas paru clair au début de mes recherches. Dans ce qui précède, j’ai parlé de l’effort des physiciens à essayer de trouver une théorie commune aux deux grandes théories à l’heure actuelle : la théorie de la relativité générale, théorie purement géométrique et qui régit les particules dans l’infiniment grand ; et la théorie quantique, théorie qui régit l’infiniment petit et qui n’est pas géométrique. Les physiciens ont déjà constaté que ces deux théories se chevauchent étroitement dans certains cas particuliers (je pense par exemple au phénomène d’évaporation des trous noirs qui n’est explicable que par la mécanique quantique et surtout grâce au fameux principe d’incertitude d’HEISENBERG)…ce qui permettrait de penser qu’il existe bien une et unique force qui englobe ces deux théories apparemment incompatibles. Mais d’un autre coté, il y a aussi les quatre grandes interactions que l’on connaît, soit les interactions faible, forte et électromagnétique, auxquelles on rajoute la gravitation. L’unification de celles-ci en une seule théorie (dont le candidat le plus cohérent semble être à l’heure actuelle la théorie des supercordes dont je parlerai dans la suite) et la précédente tentative d’unification sont bien une seule et même tentative d’unification.

1. Le modèle standard

Le modèle standard est un cadre théorique qui décrit les interactions électromagnétique, faible et forte. Selon ce modèle, ces trois interactions seraient intimement liées les unes aux autres de la même manière que le sont les interactions électromagnétique et faible dans ce que l’on appelle l’interaction électrofaible. Dit autrement, les interactions électromagnétique, faible et forte seraient des manifestations différentes d’une même interaction qui, à la suite de brisures spontanées de symétries, se serait différenciée. Cette différenciation se serait opérée en deux étapes :

1. Première brisure spontanée de symétrie à une énergie de 10¹⁶GeV résultant en la différenciation des interactions forte et électrofaible,

2. Seconde brisure spontanée de symétrie à une énergie de l’ordre de 10³ GeV résultant en la différenciation des interactions électromagnétique et faible (modèle de Glashow-Salam-Weinberg).

Cependant, le modèle standard ne décrit la super-interaction qui fédérerait les interactions électromagnétique, faible et forte. Il se contente de fournir une explication possible de la différenciation de cette interaction plus fondamentale. Dans le modèle standard, chaque interaction sous-jacente (fédérerait les interactions électromagnétique, faible et forte) conservent leurs propriétés intrinsèques.

Nous avons vu que l’interaction forte pouvait être modélisée comme un champ de jauge dont le groupe de représentation est SU(3) (rotations dans l’espace). De la même façon, l’interaction électrofaible peut être représentée par le groupe U(1) x SU(2) (rotations dans le cercle et dans le plan). Le modèle standard fait la synthèse de l’ensemble en proposant des symétries locales (ou de jauge) dans le cercle, le plan et l’espace. Le groupe de représentation est alors U(1) x SU(2) x SU(3). On le voit, les symétries de chaque interaction sous-jacente sont conservée dans la nouvelle interaction unifiée.

Le modèle standard permet de rendre compte de la plupart des phénomènes observés à ce jour, c'est-à-dire à des niveaux d’énergie de l’ordre de 10³GeV. De plus, comme toute théorie de jauge, il est renormalisable, c'est-à-dire que les quantités infinies qui apparaissent dans les équations s’annulent mutuellement pour donner des résultats finis, donc calculables et physiquement observables.

Le modèle standard constitue à ce titre une grande avancée de la physique théorique mais reste un ensemble incomplet qui ne permet pas de donner véritablement un cadre unifié pour les interactions électromagnétique, faible et forte. Cette étape suivante sera franchie par les théories dites de grande unification ou Grand Unified Theories (GUT).

a) Les GUT (Grand Unified Theories)

Il existe plusieurs théories ayant pour objectif d’unifier les interactions électromagnétique, faible et forte. Cependant, nous n’allons pas toutes les passer en revue. Nous nous limiterons à la plus "populaire" d’entre elles : la théorie SU(5).

L’idée directrice des GUT est de réduire encore le nombre de particules vraiment fondamentales. Avec le modèle standard, le zoo des particules fondamentales se limitait

· aux leptons (électron, neutrino électronique, muon, neutrino muonique, tau, neutrino tau) et leurs anti-particules,

· aux quarks (quarks u, d, s, c, b, t) et leurs anti-quarks,

· aux bosons des interactions (photon, Z⁰, W+, W-, gluons).

Toutes les particules observées sont alors soit des leptons, soit composées de quarks. A noter que les leptons et les quarks appartiennent à la famille des fermions (particules de spin demi-entier).

Bien que le nombre de particules est très réduit par rapport à la situation qui prévalait dans les années 60, les physiciens ne pouvaient se satisfaire pour autant de l’existence de deux familles de fermions distinctes : les leptons et les quarks. Cette distinction ne peut s’expliquer par les théories existantes elles-mêmes mais nécessite d’être posée de façon ad hoc.

Les GUT recherchent de nouvelles symétries, englobant celles du modèles standard et les étendant bien au delà de ce qui est du domaine observable par l'expérience (les niveaux d'énergie auxquels apparaissent ces nouvelles symétries se situent aux alentours de 10¹⁶ GeV ce qui est très loin des possibilités expérimentales d'aujourd'hui). La symétrie de base des GUT repose sur l'invariance des propriétés de la nature par permutation d'un lepton et d'un quark. Aux niveaux d'énergies auxquels intervient cette nouvelle symétrie (10¹⁶ GeV et au delà) les quarks et les leptons deviennent identiques. Au dessous du seuil des 10¹⁶ GeV, les quarks et les leptons deviennent "différents" c'est-à-dire que leur comportement physique est distinct. La symétrie qui permet de confondre quark et lepton est donc spontanément brisée au-dessous du seuil d'énergie de 10¹⁶ GeV.

b) Vers un univers supersymétrique

Finalement, les théories de jauge et la tentative d'unification des interactions nous enseignent un fait majeur : la symétrie de l’univers croit avec les énergies mises en jeu dans les interactions entre les particules. Mais rappelons nous que l’augmentation de l’énergie nous rapproche des conditions physiques du « big bang ». Donc, on en conclut que plus l’on se rapproche des conditions physiques du « big bang », plus l’univers est riche en symétries.

Dit autrement, si l’on part de l’instant du « big bang », on constate qu’au contraire les symétries vont se briser successivement au fur et à mesure que l’univers s’étend et se refroidit. En d’autres mots, il perd en symétries au fil du temps.

Les GUT ont pour objectif d’unifier les interactions faibles, forte et électromagnétiques. Il manque dans cette énumération une interaction d’importance majeure : la gravitation !

Guidés par la démarche testée dans l’édification de la théorie de l’interaction électrofaible, de celle du modèle standard et des GUT, les physiciens ont déduit que l’incorporation de la gravitation au corpus des interactions ou en d’autres termes, l’unification de l’ensemble des interactions, nécessitait un plus grand niveau de symétrie encore. Ce niveau de symétrie ultime devrait non seulement permettre de permuter n’importe quel particule avec n’importe quelle autre, mais en plus, il devrait indifférencier les champs de matière et celui créé par la gravitation, c'est-à-dire l’espace-temps lui même ! ! !

La recherche de cette ultime symétrie est l’objet de la théorie supersymétrique (notée SUSY).

2. Théorie de la supersymétrie et supergravité

a) La "matière-espace-temps"

La supersymétrie a pour objectif d’unifier toutes les interactions. Unifier toutes les interactions signifie en fait que toutes les entités susceptibles d’interagir jouent exactement les mêmes rôles vis-à-vis de l’interaction unifiée. Or, quelles sont les entités dont il s’agit ? On a :

· Les quanta de « matière » qui sont des fermions (particules de spin demi-entier),

· Les quanta de « force » qui sont des bosons (particules de spin entier),

· L’espace-temps au travers de la gravitation.

Dans le contexte de la théorie supersymétrique, la matière, les « forces » et l’espace-temps jouent donc des rôles symétriques et peuvent être intervertis dans les équations de la nature. C’est pour cela que certains physiciens utilise le néologisme « matière-espace-temps » pour parler des entités physiques manipulées par la théorie supersymétrique.

Concrètement, en quoi cela consiste ?

b) Les symétries des théories supersymétriques

Les symétries auxquelles satisfont les théories supersymétriques sont les suivantes :

· Invariance par permutation d’un fermion par un boson et vice-versa

· Invariance relativiste c'est-à-dire symétrie vis-à-vis des transformations de Poincaré (transformation de Lorentz + translations)

· Invariance par transformations CPT (C = inversion de Charge, P = Parité, T = inversion du Temps)

· Symétries associées à la conservation des nombres quantiques comme les charges, l’isospin, etc.

Les théories supersymétriques permettent effectivement d’unifier les quatre interactions fondamentales mais elles butent sur la valeur infinie de certains résultats. Aujourd’hui, ces théories servent de socle à la théorie des supercordes.

c) La théorie des champs

1. Qu'est-ce qu'un champ en physique classique ?

Dans la nature, de nombreux phénomènes font intervenir une action à distance comme, précisément, la gravitation, l'attraction et la répulsion électrostatiques ou magnétiques, etc. Prenons un exemple accessible à l'expérience quotidienne : l'attraction de deux aimants. Si l'on approche les pôles opposés de deux aimants, ils s'attirent. Cette attraction est d'autant plus forte que la distance qui les sépare est petite. Tout se passe comme si la "force" attractrice des aimants les entoure, cette "force" étant plus intense lorsque l'on se rapproche des aimants. On peut montrer que, pour un aimant donné, la "force" attractrice en un point donné conserve toujours la même valeur (à condition, bien sûr, de ne pas déplacer l'aimant !). Ainsi, il est possible d'associer à ce point de l'espace une valeur unique qui indique la valeur de l'intensité de la force d'attraction de l'aimant. L'ensemble des valeurs de l'intensité de la force d'attraction en chaque point de l'espace est appelé un champ. Cette définition a un caractère purement mathématique mais, comme nous l'avons vu, elle repose sur l'observation de phénomènes physiques. Les valeurs associées à chaque point de l'espace peuvent être des nombres réels (ou scalaires), des vecteurs (valeur + orientation), des tenseurs (êtres mathématiques plus complexes), etc. La figure ci-dessous représente un champ de Text Box: vecteurs.

Figure 1 : Un champ de vecteurs

Au-delà de cette définition mathématique, un champ est avant tout la manifestation d'un phénomène d'action à distance. La description que donnent les physiciens d'une action à distance consiste à dire que tous les ingrédients de cette action à distance sont déjà présents sous forme de champ. Il ne reste plus qu'à introduire le second aimant pour que l'action ait effectivement lieu. Le nom scientifique d'une telle action à distance est interaction (mot à mot : "action entre").

La description classique des champs amène la remarque suivante. Un champ est continu dans l'espace, c'est-à-dire que les variations des valeurs d'un point à un autre point infiniment voisin s'effectuent sans sauts brutaux. Au contraire, ces variations sont "douces", continues.

Les champs en physique classique possèdent également la particularité d'être définis immédiatement dans tout l'espace. Si, par exemple, la puissance de l'aimant croît brusquement, l'intensité du champ magnétique augmente alors brusquement dans tout l'espace. En d'autres mots, les variations de l'origine du champ sont répercutées immédiatement dans tout l'espace. La vitesse à laquelle les variations sont répercutées dans l'espace est donc infinie. Ce point est en totale contradiction avec le principe relativiste selon lequel aucune information ne peut se déplacer à une vitesse supérieure à celle de la lumière. Cependant, la description relativiste des champs, tout en intégrant la notion de déplacement des variations du champ à une vitesse finie (celle de la lumière) est, dans le fond, très semblable à la description classique. Ce ne sera pas le cas avec la physique quantique !

2. Qu'est-ce qu'un champ en physique quantique ?

Pour décrire le concept de champ en physique quantique, prenons l'exemple d'un électron fixe. D'après la théorie de l'électromagnétisme, l'électron crée un champ électrique autour de lui. Supposons maintenant qu'un second électron s'approche du premier. Il va être soumis au champ électrique de ce dernier. Les effets du champ électrique vont se manifester par une modification de la trajectoire et une accélération du second électron. D'un point de vue mécanique, on peut décrire l'interaction des deux électrons par un transfert d'énergie et de variables dynamiques de l'un à l'autre. Or, en physique quantique tout transfert d'énergie est réalisé par un - ou plusieurs - quantum ! En d'autres mots, l'interaction des deux électrons consiste en l'échange d'un quantum, c'est-à-dire finalement, en l'échange d'une particule.

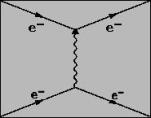
Figure 2 : Interaction entre deux électrons

La particule échangée est baptisée le quantum de l'interaction. Comme les électrons ne peuvent être distingués les uns des autres, il s'ensuit que l'interaction de n'importe quel électron avec un autre électron impliquera le même quantum d'interaction. De plus, l'interaction électrique des électrons est déterminée par leur charge électrique exclusivement. On en conclut que toute interaction causée par la charge électrique de particules implique le même quantum d'interaction que celui qui a été mis en évidence dans le cas de deux électrons. Nous verrons plus loin que ce quantum n'est rien d'autre qu'un photon !!!

La physique quantique met en jeu des énergies qui peuvent être très élevées, donc les vitesses des particules impliquées appartiennent au domaine relativiste (c'est-à-dire proches de la vitesse de la lumière). De ce fait, la physique quantique doit nécessairement intégrer la théorie de la relativité, au moins restreinte. L'un des résultats fondamentaux de la relativité restreinte est la célèbre équation E = mc² qui traduit le fait que la masse est de l'énergie et réciproquement, toute énergie peut potentiellement prendre la forme d'une masse (de particules). En physique quantique cette équation a des conséquences majeures car les quantités d'énergie déployées lors des interactions ne sont plus négligeables en comparaison de la masse des particules. Il en résulte que l'énergie impliquée dans une interaction peut se matérialiser sous forme de particules. Il s'ensuit que le nombre de particules après l'interaction peut être supérieur (parfois même très supérieur) au nombre de particules avant l'interaction. Ce phénomène est observé couramment dans les accélérateurs de particules.

L'interaction de n particules produisant m particules met en jeu des mécanismes sans doute complexes que l'on n'appréhende pas tous dans leur totalité. Aussi, les interactions sont souvent traitées comme une "boîte noire" avec des particules en entrée et d'autres en sortie. Cette "boîte noire" possède une représentation mathématique nommée la matrice de diffusion ou matrice S (S pour "scattering" qui signifie" diffusion).

Figure 3 : Interactions entre particules dans une "boite noire"

Pour passer de n particules en entrée à m particules en sortie (n et m étant différents) il faut que certaines particules disparaissent et d'autres soient créées. Comme nous l'avons dit plus haut, la mécanique quantique ne permet pas de prédire les phénomènes avec certitude mais fournit seulement les probabilités pour que ces phénomènes se produisent. Les mêmes n particules en entrée, se trouvant dans les mêmes états physiques (les physiciens disent "les mêmes conditions initiales") vont pouvoir produire une multitude de résultats différents en sortie. La mécanique quantique permet de calculer la probabilité pour que chacun de ces résultats se réalise. La situation se complique encore davantage quand on a à l'esprit qu'un même résultat en sortie peut mettre en oeuvre des mécanismes intermédiaires différents. Finalement, la probabilité d'obtenir un résultat donné en sortie est donc la somme des probabilités de l'occurrence de chaque mécanisme intermédiaire aboutissant à ce résultat. Il suffit donc de recenser l'ensemble des mécanismes intermédiaires possibles, d'en calculer la probabilité puis d'en faire la somme, pour connaître la probabilité pour qu'une interaction donnée ait lieu.

Cette procédure paraît simple sur le papier mais dans la réalité le recensement des mécanismes intermédiaires aboutit à un nombre infini ! Pour comprendre cet état de fait, reprenons le cas de notre électron et du champ électrique qu'il crée autour de lui.

Comme nous l'avons déjà expliqué, plus on se rapproche de l'électron et plus l'énergie de l'interaction croît au point que cette énergie est susceptible de se matérialiser sous forme de paires particule-antiparticule. A partir d'une certaine distance - notée d_edans le schéma ci-dessous - l'énergie est suffisante pour provoquer la création spontanée de paires électron-antiélectron. Puis avec l'accroissement de l'énergie, la formation de particules plus lourdes est possible. Toutes ces particules et anti-particules créées spontanément participent à l'interaction et doivent être prises en compte dans le calcul de la matrice de diffusion. Or, plus l'on se rapproche de l'électron, plus le nombre de paires particules-antiparticules augmente. Comme la physique moderne modélise les particules élémentaires par des objets ponctuels sans dimension, l'énergie peut donc croître jusqu'à l'infini (1/r = infini pour r = 0); le nombre de particules créées spontanément peut donc devenir infini. Ce phénomène de création spontanée de particules est à l'origine des difficultés rencontrées pour le calcul de la matrice de diffusion S (les physiciens identifient ces difficultés en parlant des "divergences de la matrice de diffusion").

Figure 4 : Energie disponible à la périphérie d'un électron

Figure 5 : Création spontanée de paires de particule-antiparticule à la périphérie d'un électron.

Les physiciens sont cependant parvenus à mettre au point une technique mathématique permettant de supprimer les termes infinis dans le calcul de la matrice de diffusion (qui donne, rappelons-le, la probabilité pour qu'une interaction ait lieu). Cette technique s'appelle la renormalisation. La renormalisation a été appliquée avec succès à l'interaction électromagnétique mais cette technique ne fonctionne pas avec toutes les interactions.

3. Les théories des cordes

a) Introduction

Quintessence moderne des efforts des physiciens pour comprendre la structure de la matière et ses interactions fondamentales, la "théorie des cordes et des supercordes" a ouvert la voie à une investigation de questions aussi essentielles que la dimensionnalité de l'espace-temps, la grande unification ou l'évolution de l'Univers. Les théoriciens du SPhT contribuent de façon active, à la fois à la caractérisation des théories invariantes conformes qui sous-tendent la théorie des cordes, à sa renormalisation et à la construction explicite de modèles de cordes à 4 dimensions.

La théorie des cordes sommeillait depuis plus de quinze ans quand elle s'est trouvée brusquement propulsée au premier plan de l'actualité scientifique. En 1984, deux théoriciens, Michael Green et John Schwarz, ont alors montré qu'elle pouvait fournir une nouvelle voie d'accès à un problème fondamental et resté sans réponse depuis Albert Einstein : réconcilier la mécanique quantique avec la relativité générale, unifier la théorie de la gravitation avec les autres interactions fondamentales de la matière. On peut dire que c'est le début de la réalisation d'un rêve inaccessible, le fameux "champ unique" recherché en vain par le sage de Princeton dans les vingt dernières années de sa vie. Une véritable aventure conceptuelle s'engage donc, mais avec la perspective de prolongements concrets dans la mesure où les nouveaux accélérateurs de particules comme le LEP à Genève et le SLC aux Etats-Unis, pourraient bientôt ouvrir la voie des vérifications expérimentales. Cinq ans après la percée théorique, et quelque temps avant les premiers résultats expérimentaux, on peut faire un rapide et provisoire bilan dans ce domaine où se sont lancées les meilleures écoles de physique théorique du monde entier.

Figure 6 : Surface d'univers balayée par des particules en forme de corde au cours de leurs déplacements et de leurs interactions dans l'espace-temps (l'axe horizontal représente le temps l'axe vertical les dimensions d'espace). Les cordes fermées balaient des surfaces qui sont des cylindres déformés. Lorsque deux cordes se rencontrent, elles se rejoignent en formant une troisième corde : deux cylindres forment un troisième cylindre. Quand deux cordes se séparent, elles créent un trou dans la surface d'univers.

L'idée centrale de la théorie des cordes est de ne plus considérer comme constituant fondamental un objet ponctuel se déplaçant dans le temps (une particule élémentaire) mais comme un objet filiforme, une corde.

La "corde élémentaire" peut s'étirer, se tordre, vibrer, se diviser ou fusionner au cours du temps en engendrant des surfaces à deux dimensions qui vont jouer dans la mécanique des cordes le rôle des trajectoires pour les particules élémentaires (fig. 22 et fig. 23). En fait, ces cordes sont extrêmement petites, ce qui ne permet pas de les distinguer des particules élémentaires dans toute expérience directe. Ce qui est spécifique aux cordes qui obéissent aux équations de la Mécanique Quantique Relativiste, c'est qu'elles déterminent en grande partie l'Espace-Temps dans lequel elles se meuvent et les interactions auxquelles elles sont soumises !

Figure 7 : A très petite échelle les particules élémentaires ne seraient pas ponctuelles mais auraient la forme de cordes infiniment minces. L'interaction entre deux cordes s'effectuerait par l'intermédiaire de processus de "cassure" et de "collage" et elle procéderait par échange de "bouts de cordes". Conséquence importante il n'y a plus séparation entre "constituants de la matière" et "médiateurs des interactions"; il n'y a plus qu'une seule classe d 'objets, les cordes.

Il faut en effet distinguer ce qu'on appelle la "dimension intrinsèque" d'un objet comme une particule ou une corde en mouvement et la "dimension de l'espace de plongement" dans lequel elles se meuvent. Le fait nouveau, c'est le lien remarquable entre les deux. Ainsi, la théorie des cordes, dans sa première version, impliquait un espace-temps à 26 dimensions, alors que la supercorde, ou corde possédant un degré de liberté de rotation (spin), vivait dans un espace-temps à 10 dimensions. La gravitation quantique, mais aussi l'électromagnétisme et les interactions nucléaires deviennent alors de simples conséquences de la géométrie et de la quantification du mouvement de la corde. La grande intuition d'Einstein, selon laquelle la Géométrie devrait être le principe unificateur de la matière et de ses interactions, et qui fut à la base de ses découvertes des théories relativistes, prouve une nouvelle fois sa fécondité.

Dès les premières études sur la théorie des supercordes, il est apparu une transformation radicale du rôle de l'espace-temps : de nouvelles dimensions spatiales (six) étaient requises et il fallait imaginer un processus de "compactification" de ces dimensions supplémentaires pour comprendre leur absence à l'échelle expérimentale, même microscopique. A l'échelle où la gravitation devient unifiée avec les autres interactions, ces dimensions peuvent prendre une réalité tangible.

Cette conception s'est depuis lors encore modifiée, car la structure de l'espace-temps dans lequel se meut la supercorde apparaît encore plus versatile puisqu'elle admet plusieurs géométries différentes (de sphère, de tore ou plus complexes encore) ou peut correspondre à des géométries qui peuvent fluctuer. Le concept qui a progressivement émergé est celui d'une propriété intrinsèque de la supercorde, non dépendante de son "plongement" : l'invariance conforme, c'est-à-dire l'invariance dans les transformations d'échelle locale. C'est comme si en chaque point de l'espace-temps, la corde pouvait s'étirer ou se froncer sans changer ses propriétés observables. Et c'est cette propriété serpentine qui caractériserait au mieux l'espace de plongement. D'une certaine manière, la boucle est bouclée : déjà rendue conceptuellement caduque (mais pas en pratique bien sûr) par la Relativité, la conception newtonienne d'un espace-temps intangible dans lequel se meuvent les objets est remplacée par une définition intrinsèque venant de l'objet lui-même, de l'espace dans lequel il se meut. Mais parmi tous les "espaces invariants conformes", lequel se trouve choisi par les équations de la supercorde ? La question reste actuellement en suspens.

Elle fait suite à une première étape qui permet de recenser et étudier tous les espaces admissibles. Nul besoin d'en souligner l'enjeu ! Il s'agit rien de moins que de comprendre pourquoi ce bas-monde "vit" en quatre dimensions et peut-être de saisir les clés profondes de notre univers. Beaucoup d'obstacles sont encore à franchir mais pourquoi se priver du plaisir de rêver avec notre vieil et respecté ami Einstein !

Il existe un grand nombre de théories des cordes, dont deux seulement semblent les plus proches de la réalité. Elles reposent toutes sur l'idée de ne pas considérer les entités élémentaires de la physique comme des particules ponctuelles (de dimension 0) mais des cordes qui formeraient des boucles d'une taille finie, de l'ordre de la longueur de Planck. Ces cordes vibreraient comme des cordes de violon, et des différents modes de vibration donneraient naissance aux spins 0,,,... et aussi dans les versions supersymétriques aux spins 0,,,... La physique changerait de nouveau son paradigme, avec des entités élémentaires qui ne seraient plus des particules ponctuelles mais des cordes minuscules. La théorie mathématique utilisée est la théorie des surfaces de Riemann à deux dimensions, les quatre dimensions de l'espace et du temps n'émergeant que comme concepts secondaires.

Une corde typique serait si petite qu'il faudrait en mettre 10²⁰ bout à bout pour atteindre le diamètre d'un simple proton. Il n'existe sur Terre aucun moyen de tester en laboratoire de façon expérimentale la structure de la matière à cette échelle, il faudrait pour cela un accélérateur de particules plus grand que la Terre elle-même. Alors que le chemin d'une particule normale dans l'espace temps est une ligne (ligne d'univers), le chemin d'une corde sera une surface bidimensionelle (feuille d'univers), une bande ou un cylindre selon le type de corde. Deux morceaux de cordes peuvent s'ajouter pour former une seule corde. De même, un morceau de corde peut se diviser en 2 cordes. Ainsi, l'émission ou l'absorption d'une particule par une autre peut se traduire en terme de "cordes" par la division ou la jonction de cordes.

Les théories des cordes semblent cependant n'être valables que si l'espace temps possède 10 ou 11 dimensions au lieu de nos 4 habituelles! Si elles existent pourquoi n'en voyons-nous que 4, 3 pour l'espace et une pour le temps? En fait, on suppose que les autres dimensions sont courbes dans un espace de très petite taille ; et puis d’ailleurs, nous autres simples humains, avons été habitués à notre petit espace à trois dimensions auquel s’ajoute le temps. Plus de quatre dimensions nous seraient donc de toute façon inconcevable mentalement.

En fait, on imagine que dans un univers primitif toutes les dimensions étaient sous cette forme, c’est à dire de très petite taille (de l’ordre de 10^-30 au mieux…) et que certaines dimensions (les quatre que nous voyons) se sont ouvertes, d’où la différence entre les cordes dites fermées et celles dites ouvertes dont nous reparlerons un peu plus bas.

b) La théorie de VENEZIANO

Historiquement, la théorie des cordes a été élaborée par VENEZIANO en 1968 pour tenter d’expliquer le confinement des quarks dans les hadrons. Veneziano avait introduit les cordes pour tenter d’expliquer pourquoi les quarks restaient confinés dans les baryons et les mésons. Les cordes jouaient le rôle de « ressorts » tendus entre les quarks, les maintenant ainsi dans un espace confiné. Avec la construction de la chromodynamique quantique, la théorie des cordes fut abandonnée, cependant certains résultats théoriques éveillèrent l’intérêt des physiciens. En effet, en 1969 SCHWARZ et SCHERK montrèrent que les cordes fermées, c'est-à-dire en forme de boucle se comportaient comme des particules de masse nulle et de spin 2. Par conséquent, les cordes fermées n’étaient rien d’autre que des gravitons! La théorie des cordes enfermait donc en elle-même la gravitation, sans devoir l’introduire de façon ad hoc.

Figure 8 : Les cordes dans un hadron

c) Les deux types de cordes

Deux types de cordes sont envisageables : ouverte ou fermée. Une corde typique serait si petite qu'il faudrait en mettre 10e20 bout à bout pour atteindre le diamètre d'un simple proton. Il n'existe sur Terre aucun moyen de tester en laboratoire de façon expérimentale la structure de la matière à cette échelle, il faudrait pour cela un accélérateur de particules plus grand que la Terre elle-même.

Alors que le chemin d'une particule normale dans l'espace temps est une ligne (ligne d'univers), le chemin d'une corde sera une surface bidimensionelle (feuille d'univers), une bande ou un cylindre selon le type de corde. Deux morceaux de cordes peuvent s'ajouter pour former une seule corde. De même, un morceau de corde peut se diviser en 2 cordes. Ainsi, l'émission ou l'absorption d'une particule par une autre peut se traduire en terme de "cordes" par la division ou la jonction de cordes.

Figure 9 : Les deux types de cordes, ouverte ou fermée

Ainsi, dans un modèle proposé en 1988, la lumière, décrite par des cordes ouvertes, peut se propager dans les trois dimensions qui nous sont familières, alors que la gravitation, représentée par des cordes fermées, peut se propager dans les dimensions parallèles envisagées par la théorie des cordes.

4. La théorie de KALUZA-KLEIN (1919-1930)

L'idée d'un nombre de dimensions supérieur à 4 apparaît dans les années 1920 avec le mathématicien germano-polonais Theodor KALUZA dès 1919 et le physicien suédois Oskar KLEIN dès 1926 qui ont tenté d’unifier de manière géométrique (la théorie de la relativité générale permettant d’interpréter la gravitation comme une déformation de l’espace-temps causée par la présence de matière et/ou d’énergie, la gravitation se ramène alors à un phénomène purement géométrique) les interactions électromagnétique et gravitationnelle à partir du formalisme de la relativité générale. Les équations de celle-ci telles que formulées par A. Einstein, ne parvenant pas à fournir une telle description géométrique pour l’électromagnétisme, Kaluza et Klein ont alors eu l’idée de rajouter une cinquième dimension à l’espace-temps et de façon très surprenante, ils parvinrent à un résultat satisfaisant.

Bien évidemment, cette cinquième dimension n’a jamais été observée de par ses dimensions, mais Kaluza et Klein proposèrent que cette dimension additionnelle pouvait être enroulée sur elle-même en tout point de l’espace dans un cylindre dont le diamètre serait de l’ordre de 10^-35m.

Mais vers 1930, la théorie Kaluza-Klein tomba dans l'oubli ou plutôt s'effaça devant la déferlante de la mécanique quantique.

Les physiciens mathématiciens sont très intéressés par les implications de cette théorie des cordes : tout en fournissant une explication du comportement connu de particules comme les électrons et les protons, elle donne une description de la gravitation en termes de comportement de cordes vibrantes ayant la forme de boucles. De nombreux physiciens estiment que les supercordes constituent donc le meilleur espoir de pouvoir développer un jour une "théorie du tout" fondamentale. Les physiciens mathématiciens sont cependant très intéressés par les implications de la théorie des cordes : tout en fournissant une explication du comportement connu de particules comme les électrons et les protons, elle donne une description de la gravitation en termes de comportement de cordes vibrantes ayant la forme de boucles. De nombreux physiciens estiment que les supercordes constituent donc le meilleur espoir de pouvoir développer un jour une "théorie du tout" fondamentale.

Les différentes particules que nous connaissons apparaîtraient alors comme différents modes de vibration d'une corde (de la même façon que chaque mode vibration d'une corde de guitare correspond à une note). La multiplicité des théories pose la question : une des théories est-elle plus exacte que les autres? La réponse fut apporté grâce au travaux de plusieurs équipes dont notamment de E. Witten. En fait chacune des théories est un cas particulier d'une théorie plus générale utilisant la supersymétrie.

Selon la théorie de Kaluza-Klein, la symétrie propre à l’électromagnétisme - rotations dans un cercle ou groupe U(1) - serait réalisée dans la cinquième dimension qu’ils ont ajoutée. Dans notre espace-temps à 4 dimensions, cette symétrie n’apparaît pas de façon explicite dans les équations de la relativité générale. La cinquième dimension imaginée par Kaluza et Klein joue donc le rôle de l’espace des phases de l’électromagnétisme. En quelque sorte, au travers de cette théorie, l’espace des phases de nature purement abstraite prendrait une forme réelle (bien que situé dans une cinquième dimension enroulée sur elle-même ! !). Jusqu’à présent, aucune expérience n’a permis de mettre en évidence la cinquième dimension de la théorie de Kaluza-Klein car ses dimensions sont beaucoup trop petites pour être accessibles par nos moyens technologiques.

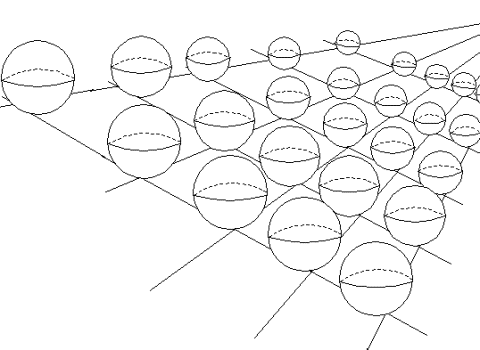
Figure 10 : Groupe U(1) dans la théorie de KALUZA-KLEIN

Cependant la supergravité à onze dimensions fut abattue en 1984, quand on lui découvrit une grave insuffisance. Dans le monde réel, la gauche et la droite ont une importance : les lois qui décrivent l'interaction nucléaire faible se modifient quand on les examine dans un miroir ; les neutrinos, par exemple, ont toujours un spin gauche. Or Edward Witten et d'autres physiciens observèrent que cette "hélicité" ne s'expliquait pas par une réduction du nombre de dimensions de onze à quatre...

5. La théorie des cordes selon Edward Witten (1990)

Physicien et mathématicien né en 1951 et enseignant à l'université de Princeton, Edward Witten est considéré comme l’un des plus éminents spécialistes de la physique théorique. En 1990, il a reçu la médaille Fields, l'équivalent du prix Nobel pour les mathématiques, pour ses modélisations de la théorie des cordes.

Sa théorie représente les particules élémentaires de la physique par des cordes extrêmement petites (100 milliards de milliards de fois plus petites qu'un noyau d'hydrogène) évoluant dans un espace étrange à 10 ou 26 dimensions, pouvant vibrer à différentes fréquences ou "résonances". Pour décrire les mouvements vibratoires d'une corde, il faut représenter un espace avec un grand nombre de dimensions. La topologie (science de l'"étude des lieux" et qui est une sorte de "géométrie de situation") joue ici un rôle majeur car elle permet d'imaginer comment, à l'intérieur de ces cordes, on peut voyager dans des mondes aux dimensions différentes.

L'intérêt de la théorie des cordes pour les théoriciens de la physique est qu'elle surmonte et par là même unifie les deux grandes théories de la physique moderne, celle de la relativité générale et celle de la mécanique quantique. Elle modifie notre compréhension de l'espace-temps et notamment envisage ses autres aménagements possibles.

Une théorie des cordes devrait satisfaire les conditions physiques suivantes:

Tous les objets du modèle standard, aussi bien les particules sources (les quarks et les leptons) que les messagers (comme les gluons, les photons, les W^{+ -} et Z⁰ (bosons)), ou que les Higgs devraient rentrer dans ce cadre.
Ce devrait être une théorie géométrique, puisqu'il lui faut aussi englober la théorie d'Einstein de la gravitation.
Elle devrait décrire la gravité sans aucun infini.

Remplir ces trois conditions tiendrait du miracle, mais ce miracle semble bien être en train de se produire, tout au moins dans un espace-temps à dix dimensions où une théorie unique des supercordes semble s'être fait jour, à la suite des travaux de GREEN et SCHWARTZ, en automne 1984.

L'espace-temps qui émerge de cette théorie des cordes unique ayant dix dimensions, il faudrait une "compactification" de six dimensions pour retomber dans notre espace-temps. Et il restera encore à descendre de la masse de Planck jusqu'aux particules W et Z, soit environ 10² fois la masse du proton. Malheureusement, l'unicité qui rendait la théorie des cordes si attachante à dix dimensions ne semble pas survivre au retour à quatre dimensions: dans ce cadre, un million de théories au moins semblent aussi défendables les unes que les autres. C'est un obstacle théorique que les cordes doivent maintenant affronter (sans parler du problème expérimental que pose la construction d'un accélérateur particulaire capable d'atteindre l'énergie de Planck (il devrait être long de dix années lumières…). De plus, les cordes pourraient-elles fournir la Théorie du Tout qui engloberait toutes les particules sources connues, les quarks, les leptons, les messagers connus et les Higgs plus toutes leurs interactions mutuelles?

6. La théorie des supercordes

a) Définition

La théorie des cordes n’était pas relativiste, c'est-à-dire que la description des cordes ne répondait pas aux exigences d’invariance par transformation de Lorentz (schématiquement, une transformation de Lorentz consiste en la contraction des distances et la dilatation des temps, conformément à des formules de transformation qu’il n’est pas nécessaire de détailler ici). Le monde de la physique entreprit de faire de la théorie des cordes une théorie relativiste donnant ainsi naissance à la théorie des supercordes.

La théorie des supercordes devaient également incorporer les dernières avancées théoriques sur le front des symétries. Ainsi, on imposa aux supercordes d’obéir à la supersymétrie, d’où le nom de supercordes.

Figure 11 : Simulation numérique d'une corde

Selon le modèle de la nouvelle théorie, les supercordes sont des cordes vibrantes de taille minuscule (~ 10^-33 cm). Il existe deux types de cordes : les cordes ouvertes et les cordes fermées.

Comme les cordes d’un instrument de musique, les supercordes peuvent vibrer selon plusieurs modes. Le premier mode comprend un ventre et deux noeuds (les ventres sont les points où l’amplitude de l’oscillation est la plus forte, les noeuds sont les points où cette amplitude est nulle, comme c’est le cas aux extrémités de la corde vibrante). Le second mode comprend deux ventres et trois noeuds. Le troisième mode trois ventres et quatre noeuds et ainsi de suite.

Chaque mode de vibration correspond à un type de particule.

La modélisation théorique des supercordes laisse la liberté de choix de certains paramètres initiaux, que l’on appelle traditionnellement des conditions aux limites. Notamment, le mouvement des extrémités des supercordes n’est pas soumis à des contraintes rigides posées a priori mais peut être considéré comme un paramètre libre de la théorie. On distingue ainsi deux types d’extrémités pour les supercordes ouvertes :

1. Celles qui peuvent se déplacer mais en étant entraînées uniquement par le mouvement de la supercorde. Elles obéissent à la condition aux limites de Neuman.

2. Celles qui restent fixes dans un hyperplan. Elles répondent à la condition aux limites de Dirichlet.

L’interaction entre deux supercordes prend une signification physique très simple. Lorsque deux supercordes interagissent, elles se fondent l’une à l’autre. Elles peuvent par la suite se scinder de nouveau en une ou plusieurs supercordes. Dans tous les cas, les processus mis en jeu sont intuitivement simples.

Figure 12 : Interaction et fusion entre deux cordes

Très schématiquement, les supercordes présentent deux intérêts majeurs :

1. Les cordes fermées possèdent les mêmes propriétés que les gravitons et peuvent donc être assimilées comme tels.

2. Les cordes sont des entités physiques ayant une dimension non nulle, alors que les particules, selon l’acceptation courante, sont ponctuelles et sans dimension.

La première propriété permet à la théorie des supercordes d’inclure naturellement la gravitation.

La seconde propriété permet de s’affranchir de toutes les difficultés inhérentes à la nature ponctuelle des particules, notamment les divergences dans le calcul des probabilités de diffusion (divergences de la matrice S). Le développement perturbatif d’une interaction selon la théorie des supercordes donne un résultat fini qui est illustré dans la figure suivante.

b) Théorie des supercordes et espace-temps

Les physiciens ont appliqué les principes de la théorie de Kaluza-Klein à la théorie des supercordes. Ainsi, pour chaque symétrie respectée par les supercordes, ils ont ajouté une dimension dans l’espace-temps dans laquelle se réalise cette symétrie. Lorsque l’on fait la somme des dimensions additionnelles nécessaires, on obtient le chiffre extraordinaire de 7! Ce qui est extraordinaire ce n’est pas la valeur particulière de ce chiffre, mais le fait que l’univers ainsi obtenu possède alors 11 dimensions…

Si l’on reprend la représentation de l’univers que propose la théorie de Kaluza-Klein, en chaque point de l’espace-temps de la théorie des supercordes 7 dimensions s’enroulent sur elles-mêmes sur une distance de 10^-33 cm. Cette longueur est précisément celle des supercordes. Pour les supercordes donc, l’univers tel qu’elles le « perçoivent » est « complet » puisqu’à leur échelle les 7 dimensions enroulées sur elles-mêmes sont bien réelles et « palpables ».

7. Conclusion

a) Peut-il y avoir réellement une théorie unique?

En fait, il semble qu'il y ait 3 possibilités:

Il n'y a pas de théorie de l'univers, les événements ne peuvent être prédits au delà d'un certain point et arrivent au hasard et de manière arbitraire.

Cette version est défendue par certains affirmant que si un ensemble de lois décrivaient le fonctionnement de l'univers, cela enfreindrait la liberté de Dieu, fut effacé en redéfinissant le but de la physique c'est à dire: de formuler un ensemble de lois capables de prédire les événements seulement dans les limites du principe d'incertitude.

§ Il n'y a pas de théorie ultime de l'univers, juste une suite infinies de théories partielles qui décrivent l'univers plus ou moins précisément.

Cependant il semble vraiment que la séquence de théories de plus en plus raffinées doivent connaître quelques limites dans le futur. En effet, la gravité parait fournir une limites à cette séquence de "poupées russes". Si l'on avait une particule avec une énergie supérieure à l'énergie de Planck (10e10 GeV), sa masse se retrancherait elle même du reste de l'univers et formerait un trou noir. Bien sur, l'énergie de Planck représente un long chemin à partir des énergies obtenues actuellement avec nos accélérateurs (~100 GeV), mais tous laisse penser qu'une théorie universelle existe.

Il y a bien une théorie unifiée.

b) Paradoxe fondamental de la théorie de l'unification

Les notions relatives aux théories scientifiques supposent que nous sommes des êtres rationnels, libre d'observer l'univers comme nous le voulons et de tirer des conclusions logiques à partir de ce que nous voyons. Donc, si une théorie complètement unifiée existe elle est vraisemblablement capable de déterminer nos actions. Ainsi, la théorie elle même devrait déterminer l'aboutissement de notre recherche la concernant!

c) Paradoxe fondamental de la théorie de l'unification

Les notions relatives aux théories scientifiques supposent que nous sommes des êtres rationnels, libre d'observer l'univers comme nous le voulons et de tirer des conclusions logiques à partir de ce que nous voyons. Donc, si une théorie complètement unifiée existe, elle est vraisemblablement capable de déterminer nos actions. Ainsi, la théorie elle même devrait déterminer l'aboutissement de notre recherche la concernant!